Gerak Parabola adalah salah satu gerak yang
dipelajari dalam Kinematika (bagian dari Fisika yang mempelajari gerak tanpa
melihat gaya yang menyebabkan gerak tersebut).
Gerak parabola mempunyai
lintasan melengkung (kurva parabola) yang menyerupai gerak peluru ketika
ditembakkan, sehingga gerak parabola disebut juga dengan gerak peluru
(projectile motion).
Gerak parabola
sangat mudah dijumpai dalam kehidupan sehari-hari. Selain dari gerak peluru
yang ditembakkan, juga gerak dari bom atau rudal yang ditembakkan merupakan
contoh gerak parabola. Hampir semua olahraga yang menggunakan bola sebagai alat
permainan juga menggunakan prinsip gerak parabola seperti sepakbola, bola voli,
bola basket, bola tenis, dan lain-lain.
Gerak
parabola dapat diuraikan menjadi gerak horizontal dan gerak vertikal. Gerak
horizontal tidak dipengaruhi gravitasi bumi sehingga merupakan Gerak Lurus
Beraturan, (percepatan nol, kecepatan tetap), sedangkan gerak vertikal
dipengaruhi percepatan gravitasi bumi, sehingga mempunyai percepatan tetap, yaitu percepatan gravitasi bumi, a =
g = 9,8 m/s2 atau 10 m/s2 (Gerak Lurus Berubah
Beraturan).
Untuk menyelesaikan soal
gerak parabola dengan asumsi gaya gesek udara diabaikan. Berikut ini akan dibahas mengenai kecepatan dan posisi dari gerak parabola,
1. Kecepatan Awal Gerak Parabola
Pada umumnya gerak parabola diawali dengan
suatu benda yang diberi kecepatan awal dengan sudut elevasi tertentu. (Sudut
elevasi adalah sudut yang diukur dari sumbu X horizontal berlawanan arah
putaran jarum jam)
Karena kecepatan awal mempunyai kemiringan maka,
dapat diuraikan menjadi komponen kecepatan awal sumbu X (horizontal) dan kecepatan awal pada sumbu Y (vertikal), sehingga
menurut aturan trigonometri kecepatan awal (Vo) dapat diuraikan
menjadi :
Keterangan :
Vo = kecepatan awal (m/s)
Vox = komponen kecepatan awal horizontal (m/s)
Voy = komponen kecepatan awal vertikal (m/s)
ϴ = sudut elevasi (dalam derajad)
2. Kecepatan
benda pada gerak parabola
Setelah benda diberi kecepatan awal dengan sudut
elevasi tertentu, maka benda akan membentuk lintasan parabola, akan melayang
sampai titik tertinggi dan kemudian kembali lagi di tanah. Kecepatan benda akan
berubah karena ada nilai percepatan gravitasi bumi yang mempengaruhi gerak
vertikal. Sehingga komponen kecepatan yang berubah adalah pada kecepatan sumbu
Y, sedangkan komponen kecepatan pada sumbu X tetap.
Komponen kecepatan
horizontal (sumbu X) sama dengan kecepatan awal horizontal (sumbu X) yang dinyatakan dalam persamaan berikut :
Komponen kecepatan pada sumbu Y didapat dari rumus kecepatan
GLBB
V = VO +
a.t
Vy = Voy + (-g).t
Percepatan gravitasi bernilai negatif karena mengurangi
kecepatan benda pada gerak parabola, sehingga persamaan komponen kecepatan
vertikal (sumbu Y) adalah
Besar kecepatan benda yang mempunyai komponen horizontal dan komponen vertikal dapat di cari dengan persamaan :
Untuk
menentukan arah sudut kecepatan digunakan perbandingan tan :
Keterangan :
V = besar kecepatan benda (m/s)
Vx = komponen kecepatan horizontal (sumbu X)
Vy = komponen kecepatan vertikal (sumbu Y)
Voy = komponen kecepatan awal vertikal (sumbu Y)
Vox = komponen kecepatan awal horizontal (sumbu
X)
g = percepatan gravitasi bumi (9,8 m/s2 atau
dibulatkan 10 m/s2 untuk memudahkan perhitungan)
t = waktu (detik)
ϴ = sudut elevasi (derajad)
α =
arah sudut kecepatan (derajad)
3. Posisi
benda pada gerak parabola
Benda yang bergerak dalam gerak parabola dapat
diprediksikan posisinya pada setiap saat, dari mulai awal, saat di udara,
hingga tiba kembali di tanah. Posisi benda akan dianalisis pada dua dimensi,
yaitu koordinat x dan y. Sama seperti komponen vektor kecepatan, posisi gerak parabola
juga diuraikan pada posisi horizontal (rx) yang merupakan Gerak
Lurus Beraturan (GLB) dan posisi vertikal yang merupakan Gerak Lurus Berubah
Beraturan (GLBB). Berikut ini adalah persamaan untuk menganalisa posisi gerak
parabola.
Posisi horizontal (sumbu X) benda pada gerak parabola memenuhi persamaan gerak lurus beraturan (GLB) sebagai berikut :
r = ro + v.t ................................. (persamaan Gerak Lurus Beraturan
(GLB))
rx = rox + vx.t
Pada umumnya koordinat awal benda dianggap (0,0) sehingga rox
= 0 meter, dan besar kecepatan horizontal vx = vo. cos ϴ sehingga
persamaan posisi horizontal menjadi :
Posisi vertikal (sumbu Y) benda pada gerak parabola
memenuhi persamaan gerak lurus berubah beraturan (GLBB) sebagai berikut :
r = ro + (vo . t) + (½ . a . t2)
........................ (persamaan GLBB)
roy =
roy + (voy. t) – (½ . g . t2)
Pada umumnya koordinat awal benda
dianggap (0,0) sehingga roy = 0 meter, tetapi jika benda diberi
kecepatan awal dari ketinggian tertentu, maka roy merupakan tinggi
awal. Besar kecepatan awal vertikal voy = vo. Sin ϴ
sehingga persamaan posisi vertikal gerak parabola menjadi :
Keterangan :
r = posisi (meter)
ro = posisi awal (meter)
rox = posisi awal horizontal (meter)
roy = posisi awal vertikal (meter)
vo = kecepatan awal gerak parabola (m/s)
vox = komponen kecepatan awal horizontal (m/s)
voy = komponen kecepatan awal vertikal (m/s)
ϴ = sudut elevasi
t = waktu (detik)
g = percepatan gravitasi bumi (m/s2)
4. Benda saat di titik puncak
Saat berada di titik puncak, benda akan berubah arah
membelok sehingga kembali lagi di tanah. Akan di analisa jarak vertikal, jarak mendatar dan waktu saat benda mencapai titik puncak.
Di titik puncak, besar kecepatan benda
bernilai minimal. Untuk kecepatan vertikal bernilai nol, karena mengalami
perlambatan sebesar gravitasi bumi, sedangkan kecepatan horizontal tetap. Dengan pendekatan kecepatan
vertikal bernilai nol pada saat titik puncak, maka dapat dicari selang waktu
benda menempuh titik puncak (tp) sebagai berikut :
Vy = nol
Voy – (g .
tp) = 0
Vo. Sin ϴ – (g . tp) = 0
Vo . Sin ϴ = g . tp
sehingga waktu untuk mencapai titik puncak adalah :
Keterangan:
tp = waktu yang dibutuhkan untuk mencapai titik
puncak (dari titik O sampai titik P)
Vo = kecepatan awal (m/s)
ϴ = sudut elevasi
(derajad)
g = percepatan gravitasi bumi (m/s2)
Setelah mendapatkan waktu
untuk mencapai titik puncak, dapat dicari posisi vertikal (Ypuncak) dan
posisi horizontal (Xpuncak) saat benda berada di titik puncak,
dengan cara mensubtitusikan waktu tp ke dalam persamaan posisi.
Menentukan Xpuncak :
rx =
(Vo . Cos ϴ) . t
Xpuncak = Vo. Cos ϴ. tp
Untuk menyederhakan
persamaan di atas digunakan persamaan trigonometeri
sin 2ϴ = 2. Cos ϴ .
Sin ϴ
Dari persamaan
trigonometri tersebut, maka
Cos ϴ . Sin ϴ = ½.
sin 2ϴ
sehingga persamaan Xpuncak di atas menjadi
:
Keterangan :
Xpuncak =
jarak mendatar pada saat benda mencapai posisi puncak (meter)
Vo = kecepatan awal (m/s)
ϴ = sudut elevasi
(dalam derajad)
g = percepatan gravitasi bumi (m/s2)
Menentukan Ypuncak :
Untuk menentukan posisi puncak dengan cara
mensubtitusikan waktu sampai puncak (tp) ke persamaan posisi ry = roy + vo. t – ( ½ . g . t2)
Dengan menganggap roy
adalah nol (benda dilempar dari tanah, tidak ada ketinggian awal) dan posisi ry
disebut Ypuncak maka
persamaan ry menjadi :
Sehingga jarak vertikal saat benda di titik
puncak adalah :
Keterangan :
Ypuncak = jarak vertikal
ketika benda mencapai titik puncak (meter)
Voy = kecepatan awal pada komponen vertikal (sumbu Y) (m/s)
Voy = Vo . Sin ϴ
g = percepatan gravitasi bumi (m/s2)
5. Benda saat tiba kembali di tanah
Setelah mendapat kecepatan awal dengan sudut
elevasi, benda akan melayang di udara, mencapai posisi puncak dan kembali ke
tanah. Saat benda tiba di tanah kembali, akan di analisa mengenai:
a. waktu saat tiba di tanah (tT)
Pada pembahasan benda berada diposisi puncak, dapat ditentukan gerak parabola membentuk pola yang simetris, sehingga saat benda berada di posisi puncak merupakan setengah dari perjalanan. Sehingga waktu benda mencapai tanah (tT) adalah 2 kali waktu benda mencapai posisi puncak :
tT = 2. tp
Sehingga waktu yang dibutuhkan benda sampai di tanah kembali adalah :
Keterangan :
tT = waktu saat tiba di tanah kembali (detik)
vo = kecepatan awal (m/s)ϴ = sudut elevasi
g = percepatan gravitasi (m/s2)
vo = kecepatan awal (m/s)ϴ = sudut elevasi
g = percepatan gravitasi (m/s2)
b. Jarak mendatar saat tiba di tanah diukur dari posisi awal (XT)
Saat benda tiba di tanah kembali maka jarak
mendatar (horizontal) sama dengan jangkauan terjauh yang dicapai oleh benda.
Karena lintasan parabola adalah simetris, maka jarak terjauh sama dengan 2 kali
jarak mendatar saat benda mencapai posisi puncak.
XT = 2 . Xpuncak
Sehingga persamaan untuk jarak mendatar terjauh
(ketika sampai tanah kembali) adalah :
Keterangan :
XT = jarak mendatar terjauh (maksimal) saat tiba di tanah
kembali (meter)
Vo = kecepatan awal (m/s)
ϴ = sudut elevasi
g = percepatan gravitasi bumi (m/s2)
c. Kecepatan benda saat tiba di tanah
Saat tiba di tanah benda tidak langsung berhenti, kecepatan benda saat
tiba di tanah tidak nol. Hal ini dapat dibuktikan ketika benda yang menyentuh
tanak akan terdengar benturan atau tanah akan berlubang benda tiba di tanah.
Khusus untuk lemparan awal dari tanah (tanpa ketinggian awal), besar kecepatan saat benda tiba di tanah pada komponen
horizontal dan vertikal adalah sama besar dengan kecepatan awal, sehingga besar
kecepatan saat tiba di tanah adalah sama dengan kecepatan awal. Untuk arah
kecepatan vertikal saat tiba di tanah berlawanan arah dengan kecepatan awal vertikal.
VT horizontal = Vx = Vox = Vo
. Cos ϴ
VT vertikal =
- Voy = - Vo. sin ϴ
Besar kecepatan benda saat tiba di tanah adalah :
Karena kecepatan horizontal sama dengan kecepatan awal vertikal maka, besar kecepatan di tanah sama dengan kecepatan awal :
Keterangan :
VT = kecepatan saat tiba di tanah (m/s)
Vo = kecepatan awal (m/s)
Persamaan tersebut hanya berlaku untuk benda yang dilempar dari tanah (tanpa ketinggian awal)
Konsep konsep di atas adalah konsep gerak parabola secara dasar. Untuk lebih untuk memahami konsep gerak parabola perlu dikerjakan latihan latihan soal.











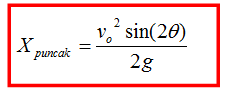






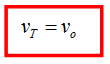
No comments:
Post a Comment